In the last chapter we learnt that the cosine rule can be used with any triangle to help us find:
-
the third side of a triangle when you know two sides and the angle between them.
-
the angles of a triangle when you know all three sides.
Remember that if $a$a, $b$b and $c$c are the side lengths of a triangle, with angle $C$C opposite the side with length $c$c, then:
$c^2=a^2+b^2-2ab\cos C$c2=a2+b2−2abcosC
$\cos C=\frac{a^2+b^2-c^2}{2ab}$cosC=a2+b2−c22ab
The patterns we study are universal, and knowing them well allows us to model and answer questions about the natural world, to explain and measure physical characteristics in a broad range of contexts.
Exploration
Scientists can use a set of footprints to calculate an animal's step angle, which is a measure of walking efficiency. The closer the step angle is to $180^\circ$180°, the more efficiently the animal walked. Knowing the step angle can help understand how an animal moved, even if they have never seen it. For example, here is a set of prints left by a dinosaur in the lower cretaceous period, with the step angle highlighted:
 |
 |
 |
This particular set of footprints has lengths $c=304$c=304 cm, $a=150$a=150 cm and $b=182$b=182 cm. We want to find the step angle $C$C to the nearest degree.
We know three side lengths, and want to find an angle, so we can use the cosine rule.
Since angle $C$C is the step angle we're trying to find then we can use this version of the cosine rule:
$\cos C=\frac{a^2+b^2-c^2}{2\times a\times b}$cosC=a2+b2−c22×a×b
Then substitute in all the values we know:
| $\cos C$cosC | $=$= | $\frac{182^2+150^2-304^2}{2\times150\times182}$1822+1502−30422×150×182 | (Substituting our values into the equation) |
| $\cos C$cosC | $=$= | $\frac{-36792}{54600}$−3679254600 | (Simplifying the numerator and denominator) |
| $C$C | $=$= | $\cos^{-1}\left(\frac{-36792}{54600}\right)$cos−1(−3679254600) | (Taking the inverse cos of both sides) |
| $C$C | $=$= | $132^\circ$132° | (Answer rounded to the nearest degree) |
Notice that the cosine ratio of the angle is negative. This indicates that the angle will be greater than $90^\circ$90°.
Example 1
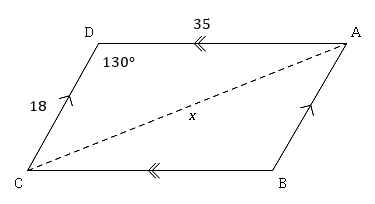
Find the length of the diagonal, $x$x, in parallelogram $ABCD$ABCD.
Write your answer correct to two decimal places.
Example 2
Dave leaves town along a road on a bearing of $169^\circ$169° and travels $26$26 km. Maria leaves the same town on another road with a bearing of $289^\circ$289° and travels $9$9 km.
Find the distance between them, $x$x, answering to the nearest km.