Area Composite Shapes

We have already had a look at combining 2D shapes together and finding the area of composite shapes.  But since then we have learnt about the areas of a whole lot more shapes.  

Let's just look at a summary of areas of 2D shapes we have looked at so far with our shape robot:

Strategies

The key skills you need to remember when thinking about composite shapes are to consider

• can the shape be considered as a larger easier shape with smaller bits missing
• can the shape be considered the sum of a number of smaller shapes

$$Area of a Rectangle =length ×width

$$A=L×W

$$Area of a Square =Side ×Side

$$A=S×S

$$area of a triangle =12​×base ×height

$$A=12​bh

$$Area of a Parallelogram =Base ×Height

$$A=b×h

$$Area of a Trapezium=12​×(Base 1 +Base 2 )×Height

$$A=12​×(a+b)×h

$$Area of a Kite=12​×diagonal 1×diagonal 2

$$A=12​×x×y

$$Area of a Rhombus =12​×diagonal 1×diagonal 2

$$A=12​×x×y

$$Area of a circle

$$A=πr2

$$Area of a sector

$$A=angle of sector360​×πr2

Worked Examples

QUESTION 1

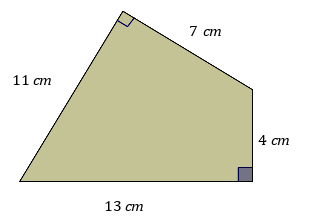
QUESTION 2