Is there a relationship between the years since purchased and the value in thousands of dollars? Explain.
Which of the lines on the graph is the line of best fit?

A line of best fit (or trend line) is a straight line that best represents the data on a scatterplot. We can use lines of best fit to help us make predictions or conclusions about the data.

We previously approximated a line of best fit by trying to balance the number of points above the line with the number of points below the line. This can result in multiple different models.

\text{Weekly growth}

\text{Height (cm)}

3 points above, 3 points below

\text{Weekly growth}

\text{Height (cm)}

5 points above, 4 points below

\text{Weekly growth}

\text{Height (cm)}

We get a more accurate line of best fit when we use technology, referred to as linear regression analysis.

Once we have found the line of best fit for a scatterplot, we can interpret the key features and use the line to predict values that don't appear in the data set.

In the context of a line of best fit, the slope-intercept form represents

\displaystyle y=mx+b

\bm{m}

the rate of change for y with respect to x

\bm{b}

the starting value of y when x is 0

For example, this graph models a plant's growth over several weeks.

\text{Weekly growth}

\text{Height (cm)}

The slope of the line y=1.21x+2.14 means that the plant is growing at a rate of 1.21 centimeters per week.

The y-intercept of 2.14 means the plant was 2.14 centimeters tall at week 0. This is feasible if the plant was not a seed when measurements began.

Besides the slope (m) and y-intercept (b), technology used for linear regression also gives us the correlation coefficient. We use the letter r to represent it. The correlation coefficient is always a number between -1 and 1. It tells us two things about the linear relationship between the variables: its strength and its direction.

Here's how to interpret the value of r:

The sign of r indicates the direction of the association.
- A positive r value means a positive association (as x increases, y tends to increase).
- A negative r value means a negative association (as x increases, y tends to decrease).
The magnitude (the absolute value) of r indicates the strength of the linear association.
- Values close to 1 or -1 indicate a strong linear relationship (points lie close to the line of best fit).
- Values close to 0 indicate a weak or no linear relationship (points are scattered far from the line).
- Values between 0.5 and 0.8 (or between -0.5 and -0.8) usually mean a moderately strong linear relationship.

It's important to remember that correlation does not imply causation. A strong correlation between two variables doesn't necessarily mean that one variable causes the change in the other.

When using technology like Desmos or a graphing calculator for linear regression (often by entering y_1 \sim mx_1 + b), the output will usually include the value of r along with the parameters m and b.

These terms describe the range in which we make predictions:

Interpolation: Prediction within the range of x-values in the data
Extrapolation: Prediction outside the range of x-values in the data

A scatterplot with interpolation from a line of good fit. Ask your teacher for more information.

A scatterplot with extrapolation from a line of good fit. Ask your teacher for more information.

Using the previous example of the plant height over time:

\text{Weekly growth}

\text{Height (cm)}

Interpolating which week the plant was 9 centimeters tall, we will solve 9=1.21x+2.14. The plant was 9 centimeters tall at 5.67 weeks.

Extrapolating the plant's height at 10 weeks, we will evaluate y=1.21\left(10\right)+2.14. The plant will be 14.24 centimeters tall at 10 weeks.

The reliability of predictions depends on the strength of the relationship, whether the data is interpolated or extrapolated, and the number of points in the data set.

A larger sample size generally increases reliability.
The strength of the correlation (r value): Predictions are more reliable when the correlation is strong (|r| is close to 1).
Interpolation vs. Extrapolation:
- Interpolation (making predictions for x-values between the smallest and largest x-values in the data) is usually more reliable than extrapolation. This is especially true if the correlation is strong or moderate.
- Extrapolation (making predictions for x-values outside the smallest and largest x-values in the data) gets less reliable the farther we go from the known data. Even with a strong correlation, the straight-line pattern might not continue forever.

Examples

Example 1

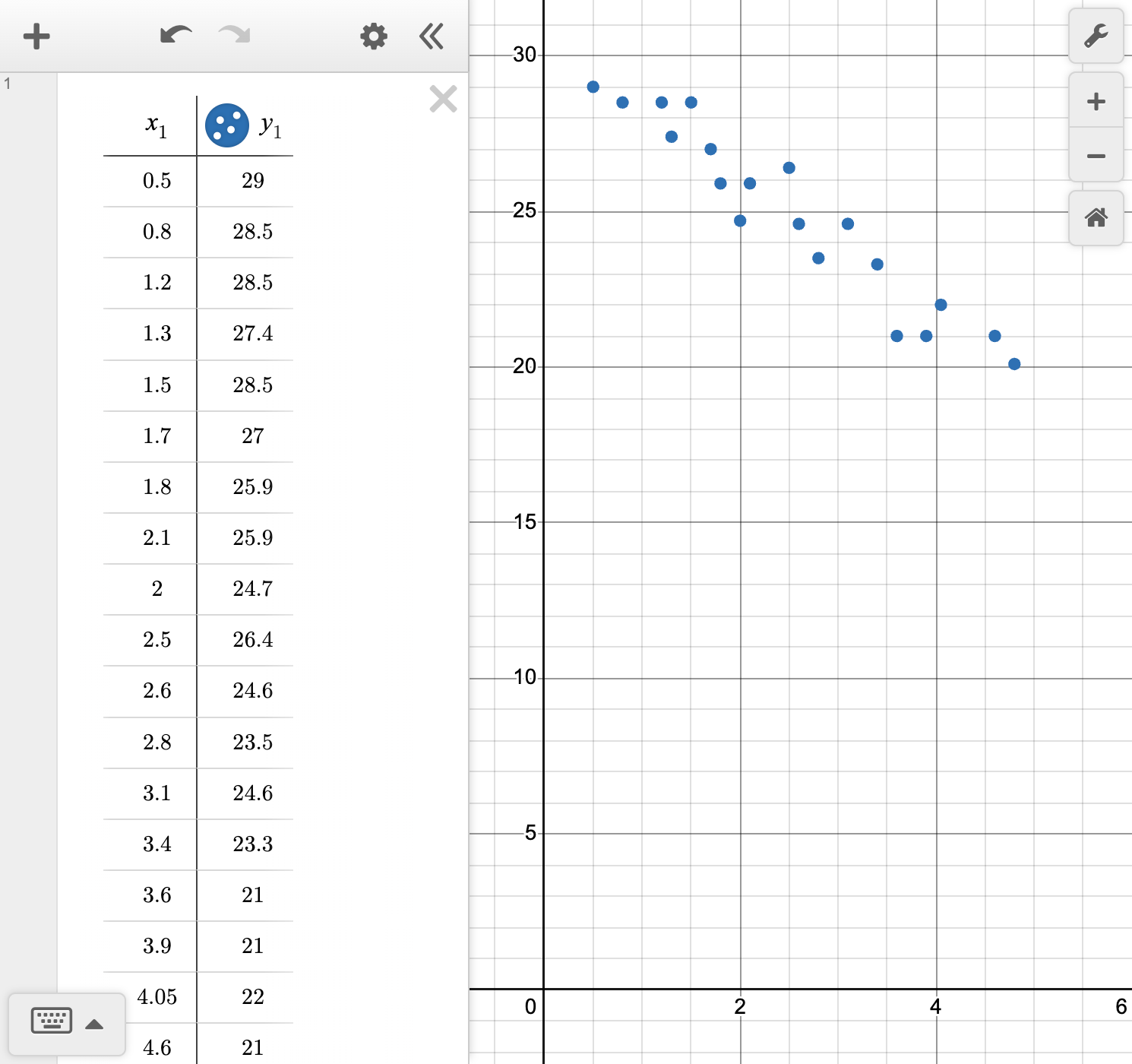
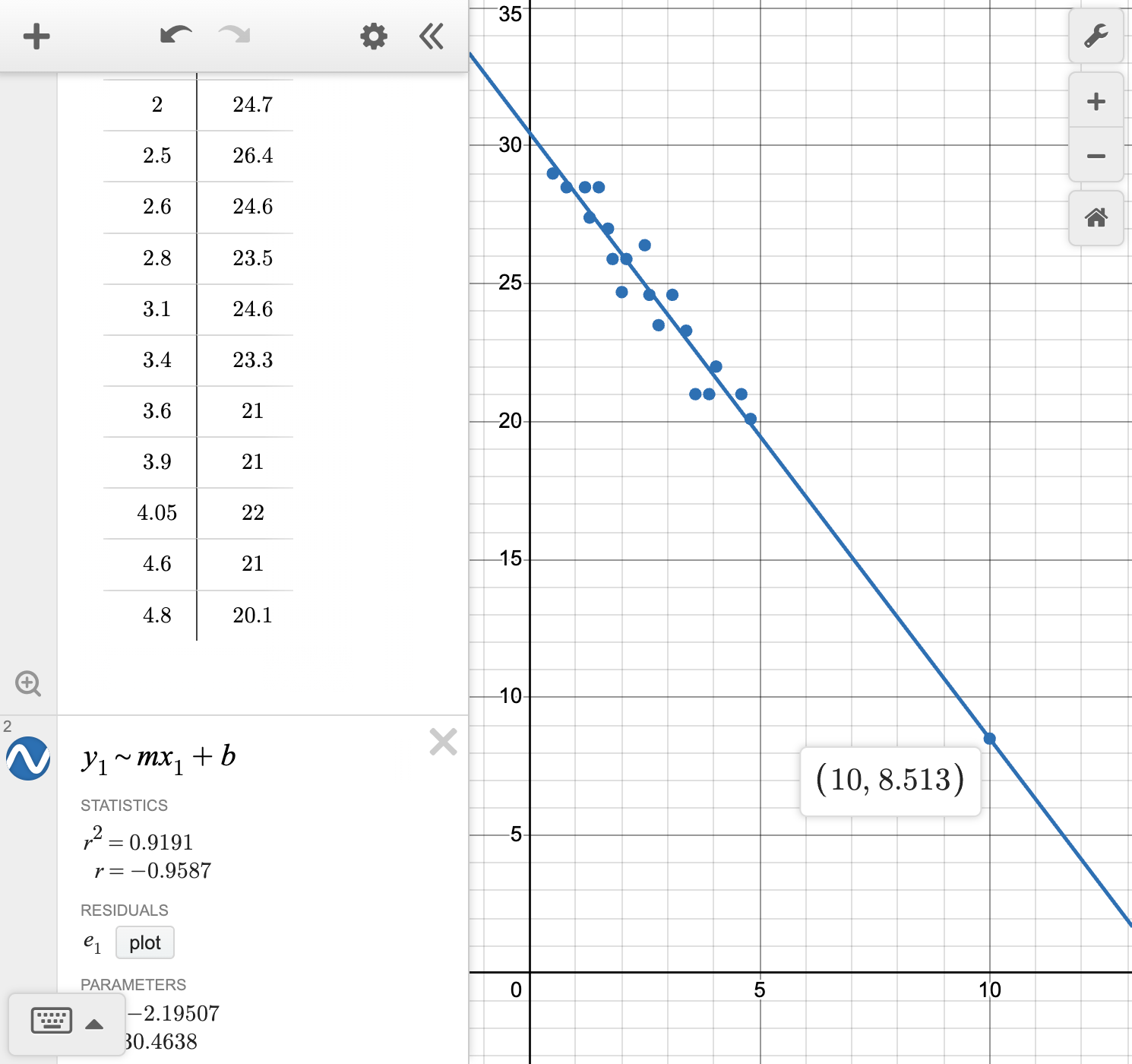
Natalia collected data to answer the question, "What is the relationship between the years since purchasing a car and its value?" Her data is shown in the table.

Time since purchase (years)	0.5	0.8	1.2	1.3	1.5	1.7	1.8	2.1	2	2.5
Value (thousands of dollars)	29	28.5	28.5	27.4	28.5	27	25.9	25.9	24.7	26.4

Time since purchase (years)	2.6	2.8	3.1	3.4	3.6	3.9	4.05	4.6	4.8
Value (thousands of dollars)	24.6	23.5	24.6	23.3	21	21	22	21	20.1

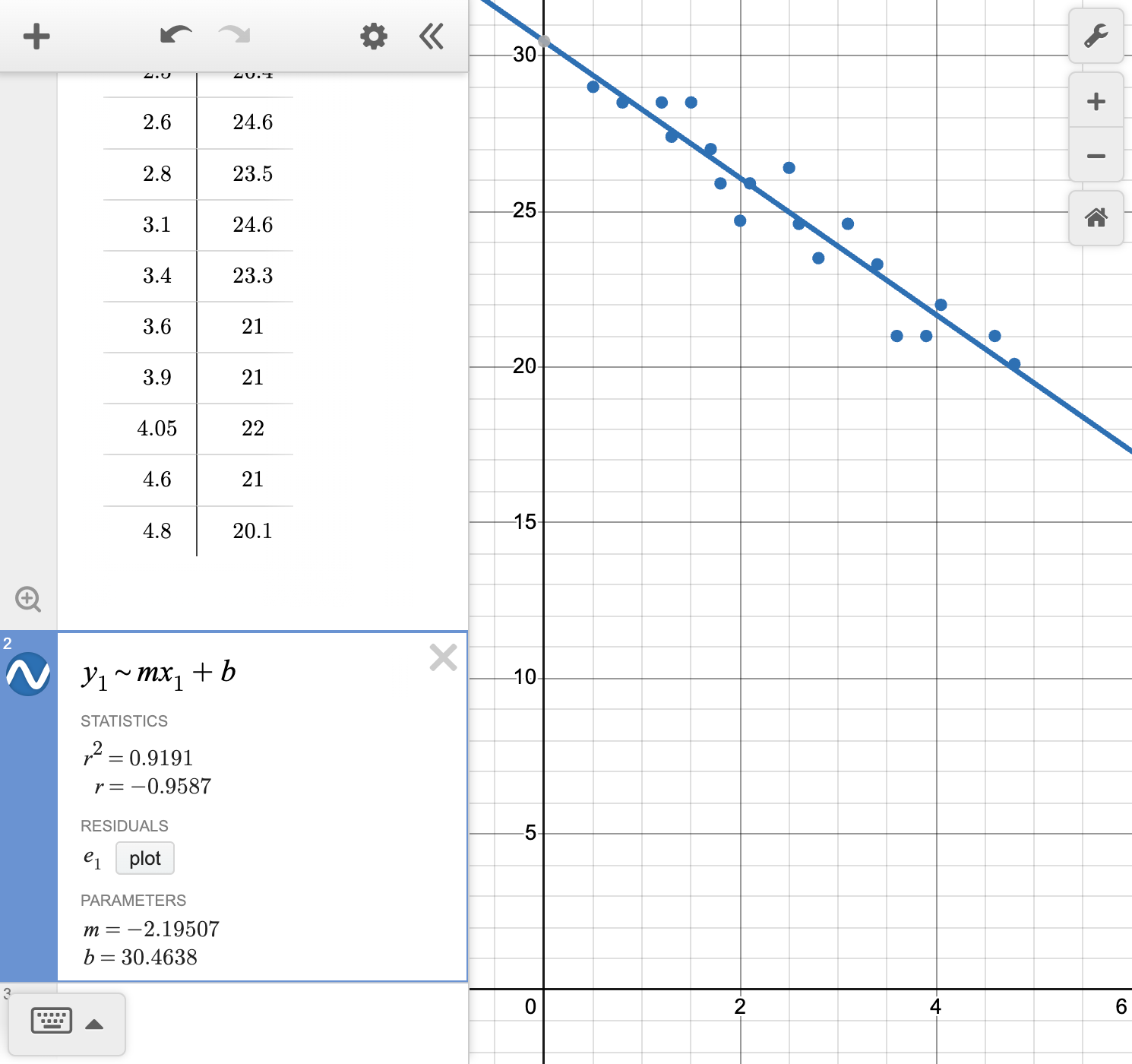
Find the equation of the line of best fit.

Worked Solution

Create a strategy

To find the equation using technology, we can follow these steps:

Click the plus sign in the top left corner of the screen, and select table.
Enter the x-values and y-values in the respective columns of the table.
In a new line beneath the table, enter the equation y_1\sim mx_1+b.

Apply the idea

Click the plus sign in the top left corner of the screen, and select table.
Enter the x-values and y-values in the respective columns of the table.
In a new line beneath the table, enter the equation y_1\sim mx_1+b.

The parameters of the equation are m=-2.19507 (which is the coefficient of x) and b=30.4638 (which is the constant, or y-intercept).

If we round the parameters to two decimal places, the equation of the line of best fit is y=-2.20x+30.46.

Reflect and check

The points are tightly clustered around the line, indicating that the relationship between the years since the car was purchased and the value of the car is strong. This means the line of best fit can be used to make relatively reliable predictions.

Remember, a strong relationship does not imply that one variable causes changes in the other. We cannot say that the year since the car was purchased causes the value of the car to decrease, as there may be other factors that affect the value of the car.

Calculate and interpret the correlation coefficient r for this data.

Worked Solution

Create a strategy

Use the same technology output from part (a) where we found the line of best fit. The output also provides the correlation coefficient, r. Interpret its value by considering its sign (direction) and magnitude (strength).

Apply the idea

Looking at the technology output from part (a):

A screenshot of the Desmos graphing calculator output for linear regression, highlighting the r value. Speak to your teacher for more details.

The correlation coefficient is given as r = -0.8702 (approximately).

Interpretation:

Direction: Since r is negative, there is a negative linear association between the time since purchase and the car's value. As the years increase, the value tends to decrease.
Strength: The value -0.8702 is close to -1. This indicates a strong linear relationship. The data points cluster closely around the line of best fit.

Reflect and check

A strong negative correlation aligns with our real-world expectation that cars generally depreciate (lose value) over time. The strength (|r| \approx 0.87) suggests the linear model is a good fit for this data within the observed range.

Interpret the slope and y-intercept of the line.

Worked Solution

Create a strategy

Use the independent and dependent variables to determine the units of the slope and y-intercept.

Car value over time

\text{Time since purchase (years)}

\text{Value (thousands of dollars)}

To help us visualize the relationship better, we can sketch the scatterplot and line of best fit, and add labels on the axes of the graph.

Remember that the y-values are in thousands of dollars. This means we will need to multiply the y-value of the slope and y-intercept by 1000 when interpreting them in context.

Apply the idea

The y-intercept of \left(0,30.46\right) means that at the time of purchasing the car, it would have a value of \$30\,460.

The slope of -2.20 means that each year, the car's value would decrease by \$2200.

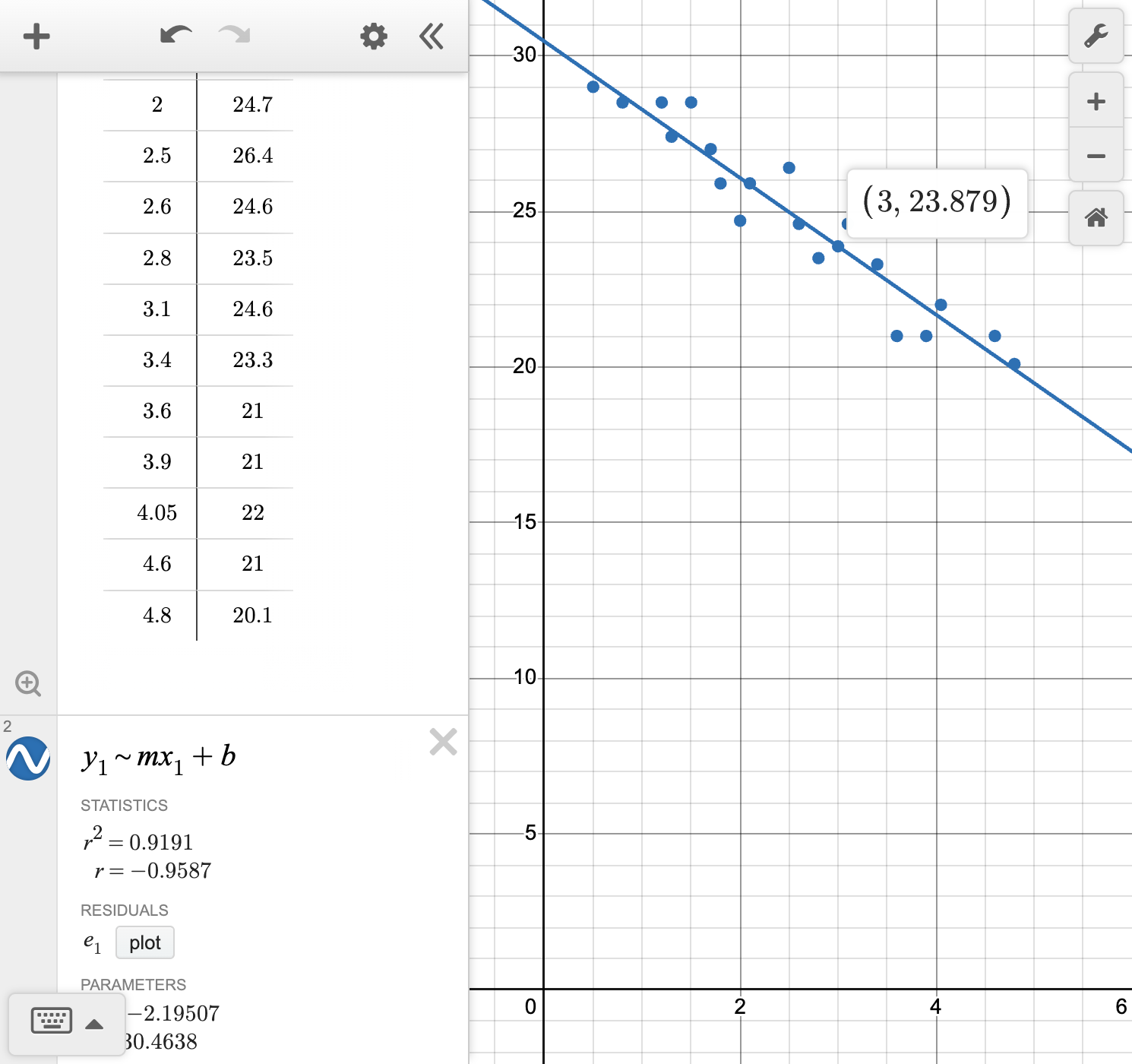
Make a prediction about the value of a car after 3 years.

Worked Solution

Create a strategy

We are given the years since the car was purchased, which is the independent variable \left(x\right), and we are looking for the value of the car, which is the dependent variable \left(y\right).

We can use the graph to estimate the y-value at x=3 or use the line of best fit to get a more accurate prediction.

Apply the idea

When we substitute x=3 into the equation, we get \begin{aligned}y&=-2.20\left(3\right)+30.46\\&=23.86\end{aligned} Based on the equation of the line of best fit, a car that is initially valued at \$30\,460 will be worth \$23\,860 three years after it was purchased.

Reflect and check

When using technology to evaluate x=3, we will get a slightly different answer. This is because the coefficients were rounded in our line of best fit. The calculator does not round the coefficients, making its result more accurate.

A screenshot of the Desmos graphing calculator showing how to use the scatterplot to predict the value of y given a value of x. Speak to your teacher for more details.

Make a prediction about the value of a car after 10 years.

Worked Solution

Create a strategy

Since 10 years after purchase is not shown on the graph, we can use the equation of the line of best fit to determine the value of a car at that time.

Apply the idea

We can use technology to find the value of y when x=10 by tracing the line of best fit.

A car that is initially valued at \$30\,460 will be worth \$8513 ten years after it was purchased.

Is the prediction for the car's value after 3 years or after 10 years more reliable?

Worked Solution

Create a strategy

To determine the reliability of the predictions, consider whether interpolation or extrapolation was used to make the prediction. Interpolation leads to a more reliable outcome than extrapolation.

We should also look at how strong the relationship is, using the correlation coefficient (r) we found in part (b).

Apply the idea

The given data ranges between x=0.5 and x=4.8. This means the prediction of the car's value after 3 years falls within the range of known data (interpolation), while the prediction after 10 years falls outside of that range (extrapolation).

The prediction of the car's value after 3 years is more reliable.

This is supported by the strong correlation (r \approx -0.87), which gives us more confidence in predictions made close to or within the data range. While the correlation is strong, extrapolation always introduces uncertainty, making the 10-year prediction inherently less reliable than the 3-year interpolation.

Reflect and check

Interpolation is generally more reliable because it involves predicting within the bounds of observed data patterns. Extrapolation assumes the observed linear trend continues indefinitely, which is often not true in real-world scenarios (e.g., a car's value won't decrease linearly forever; it might plateau or change rate). The strong correlation (r \approx -0.87) strengthens the reliability of the interpolation at 3 years. However, even with strong correlation, the extrapolation at 10 years is significantly less reliable because it's far outside the 0.5 to 4.8 year data range.

Example 2

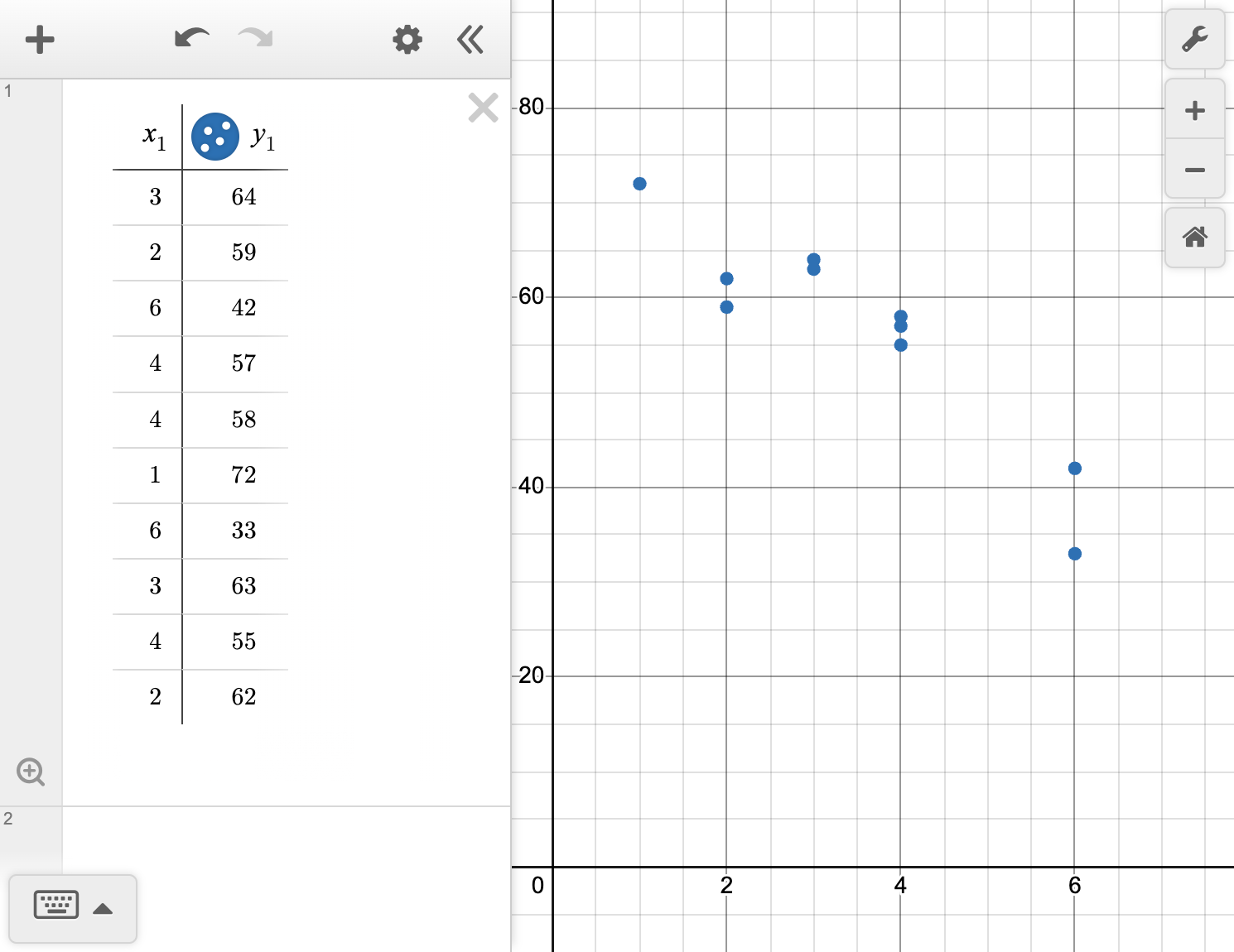
A teacher recorded the number of days since a student last studied for an exam and their score out of a possible 80 points on the exam.

Days since studying	3	2	6	4	4	1	6	3	4	2
Exam score	64	59	42	57	58	72	33	63	55	62

Formulate an investigative question that can be answered by the data.

Worked Solution

Create a strategy

The question should be focused on the relationship between the variables represented by the data. The independent variable is the number of days since studying, and the dependent variable is the score on the exam.

Apply the idea

One possible question is, "How does the number of days since a student last studied impact their exam score?"

Reflect and check

Other possible questions are:

What is the relationship between the number of days since a student last and their exam score?
How many days prior to the exam should a student study to increase their exam score?
If a student studies on the same day as the exam, what is their expected score on the exam?

Describe the relationship between the number of days since studying and the exam score.

Worked Solution

Create a strategy

To describe the relationship, we should construct a scatterplot to get a visual of the data. Then, we will consider the form (linear or nonlinear), strength (strong, moderate or weak), and direction (positive or negative).

Apply the idea

\text{Days since studying}

\text{Score }

The data appears to have a strong, negative, linear relationship.

Relating this back to the context, we can say that as the number of days since a student last studied increases, and their score on the exam tends to decrease.

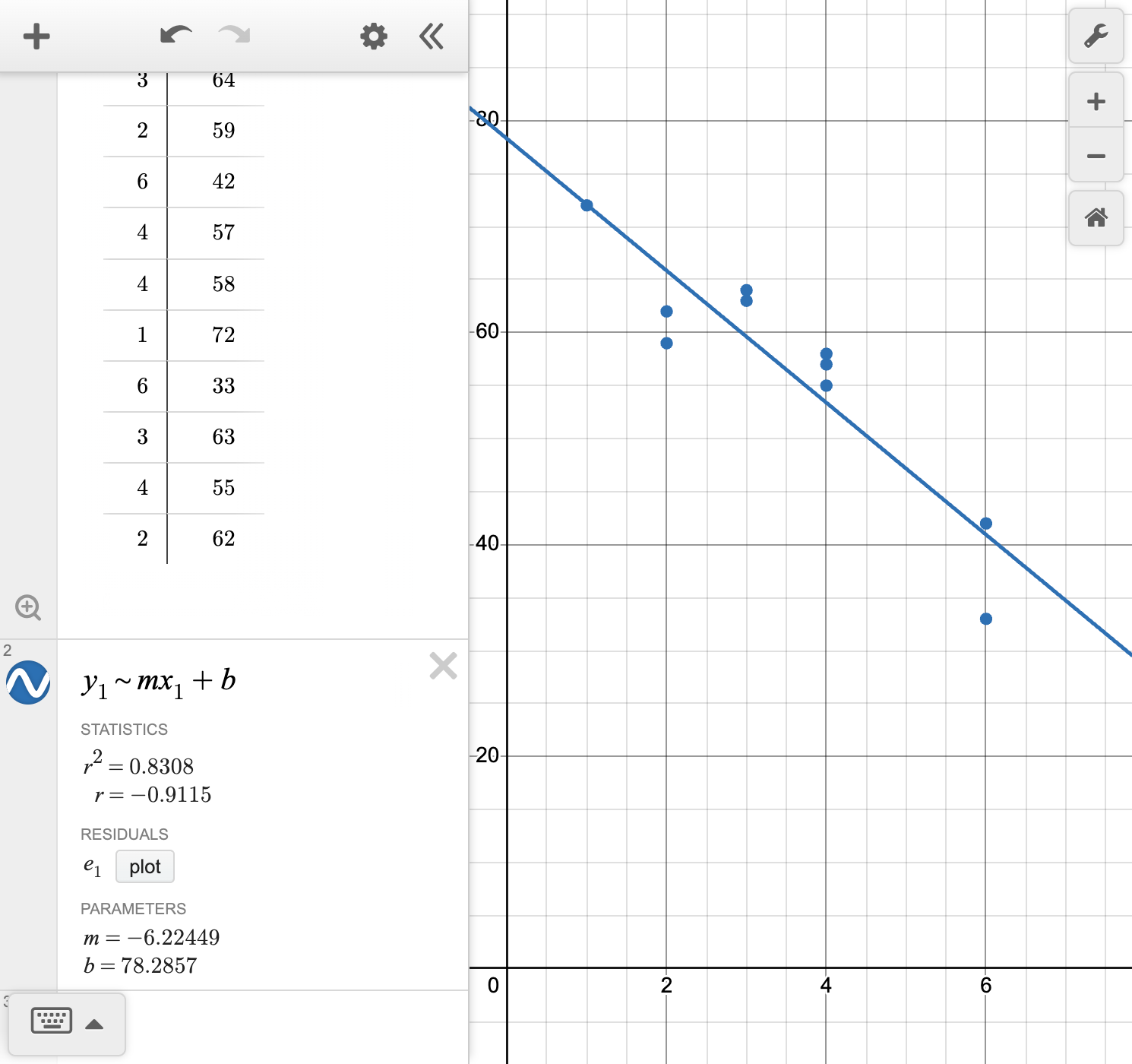
Calculate the line of best fit using technology.

Worked Solution

Create a strategy

To find the equation using technology, we can follow these steps:

Click the plus sign in the top left corner of the screen, and select table.
Enter the x-values and y-values in the respective columns of the table.
In a new line beneath the table, enter the equation y_1\sim mx_1+b.

Apply the idea

Click the plus sign in the top left corner of the screen, and select table.
Enter the x-values and y-values in the respective columns of the table.
In a new line beneath the table, enter the equation y_1\sim mx_1+b.

The equation of the line of best fit is y=-6.2245x+78.2857

Reflect and check

If the instructions do not specify to round the coefficients, it is best to include all the digits given by the calculator. This increases the accuracy of the model and the predictions.

Calculate and interpret the correlation coefficient r for this data.

Worked Solution

Create a strategy

Use the technology output from part (d) which calculated the line of best fit. Locate the correlation coefficient, r, provided by the technology. Interpret its sign for direction and its magnitude for strength.

Apply the idea

From the technology output in part (d):

The correlation coefficient is r = -0.8937 (approximately).

Interpretation:

Direction: The negative value indicates a negative linear association. As the number of days since studying increases, the exam score tends to decrease.
Strength: The value -0.8937 is very close to -1, indicating a strong linear relationship between the number of days since studying and the exam score.

Reflect and check

The strong negative correlation aligns with the conclusion in part (c) and the interpretation of the slope in part (f). It suggests that the linear model y=-6.2245x+78.2857 is a good representation of the relationship within this dataset.

Answer the question formulated in part (a).

Worked Solution

Create a strategy

To answer the question, "How does the number of days since a student last studied impact their exam score?", we can describe the direction of the linear relationship. To be more specific, we can interpret the slope of the line in context.

In part (d), we found the equation of the line of best fit to be y=-6.2245x+78.2857, which tells us the slope is -6.2245.

Apply the idea

As the number of days since a student last studied increases, their exam score decreases. More specifically, for each additional day since a student last studied, their exam score is expected to decrease by about 6 points.

Reflect and check

Matching the rise and run of the slope to their respective units can help us interpret its meaning in context.\text{slope}=\dfrac{\text{rise}}{\text{run}}=\dfrac{\text{change in }y}{\text{change in }x}=\dfrac{-6.2245}{1}

\text{Days since studying}

\text{Score }

The y-values represent the exam score, which is the "rise" of the slope. The x-values represent the number of days since studying, which is the "run" of the slope.

Since the slope is negative, it represents a decrease of 6.2245 in the exam score for every 1 day since studying.

If a student studied the same day as the exam, what would we expect their score to be?

Worked Solution

Create a strategy

If the number of days since a student last studied is 0, then their exam score is the y-value of the y-intercept.

Apply the idea

The y-intercept tells us that a student who has studied on the day of the exam has a predicted score of 78.2857, according to the linear model.

Reflect and check

Although this prediction uses extrapolation (since x=0 is outside the data range of 1 to 6 days), it is extrapolating to a value very close to the observed data. Given the strong negative correlation found in part (e) (r \approx -0.89), this prediction is likely relatively reliable, assuming the strong linear trend holds just outside the measured range.

Idea summary

A line of best fit for a set of data can be used to interpret a given situation and make predictions about values not represented by the data.

A line of best fit has an equation of the form y=mx+b. We can use technology to perform the linear regression analysis.

In the context of a line of best fit, the slope-intercept form represents

\displaystyle y=mx+b

\bm{m}

the rate of change for y with respect to x

\bm{b}

The starting value of y when x is 0

Technology used for linear regression also provides the correlation coefficient (r), a value between -1 and 1.

r measures the strength and direction of the linear relationship.
Sign indicates direction (positive or negative association).
Value close to 1 or -1 indicates a strong linear relationship; value close to 0 indicates a weak one.

These terms describe the range in which we make predictions:

Interpolation: Prediction within the range of x-values in the data
Extrapolation: Prediction outside the range of x-values in the data

The reliability of predictions depends on several factors, including the strength of the correlation (r), whether the prediction is an interpolation (within the data range) or an extrapolation (outside the data range), and the sample size. Predictions are generally more reliable when the correlation is strong (|r| is close to 1) and when interpolating rather than extrapolating.

Outcomes

AFDA.DA.1a

Formulate investigative questions that require the collection or acquisition of bivariate data, where exactly two of the variables are quantitative.

AFDA.DA.1b

Collect or acquire bivariate data from a representative sample to answer an investigative question.

AFDA.DA.1c

Represent bivariate data with a scatterplot using technology and describe how the variables are related in terms of the given context.

AFDA.DA.1d

Make predictions, decisions, and critical judgments using data, scatterplots, or the equation(s) of the mathematical model.

5.06 Linear regression

Ideas

Linear regression

Exploration

Examples

Example 1

Example 2

Outcomes

AFDA.DA.1a

AFDA.DA.1b

AFDA.DA.1c

AFDA.DA.1d

What is Mathspace

About Mathspace