Topics
7. Similarity
topic badge
United States of AmericaVA
Geometry

7.01 Dilations

Lesson
Practice

Dilations

Recall that a dilation is a transformation which changes the size of a figure through either an enlargement, which makes the figure bigger, or a reduction, which makes the figure smaller, by a given scale factor.

Dilation

A transformation where an image is formed by enlarging or reducing the preimage proportionally by a scale factor from the center of dilation.

There are two quadrilaterals of the same shape but different sizes. The smaller quadrilateral is in the larger quadrilateral. Dashed arrows connect the corresponding vertices.
Scale factor

The constant, k, that is multiplied by the length of each side of a figure to produce an image whose segments are k times the size of the corresponding segments in the preimage.

When performed on the coordinate plane, a dilation will have a specified scale factor as well as a specified center of dilation. If none is specified the origin is assumed to be the center of dilation.

Center of dilation

A fixed point on the coordinate plane about which a figure is either enlarged or reduced.

Consider the following dilation, where preimage A is dilated by a factor of k around point P.

A figure showing pre image A, triangle X Y Z being dilated by a factor of k around a point P. The resulting image is X prime Y prime Z prime. Speak to your teacher for more details.

  • The distance between the center of a dilation and any point on the image is equal to the scale factor multiplied by the distance between the dilation center and the corresponding point on the preimage: For example, PX'=k \cdot PX

  • The length of the image of a line segment is equal to the length of the line segment multiplied by the scale factor: For example, X'Y'=k \cdot XY

  • Notice that point P is not on any of the line segments of the preimage. In this case, the preimage and the image will be parallel.

  • Since each corresponding segment on the preimage and the image will be parallel, the angles formed where the segments meet at each vertex will have the same angle measure. Thus, corresponding angles in the image and preimage are congruent.

Coordinate form: The dilation \left(x,y\right) \to \left(kx,ky\right) takes the preimage and dilates it by a factor of k, about the origin.

If k>1, the dilation will be an enlargement, and if 0 \lt k \lt 1, the dilation will be a reduction. If k=1, the dilation maps the preimage onto itself.

Examples

Example 1

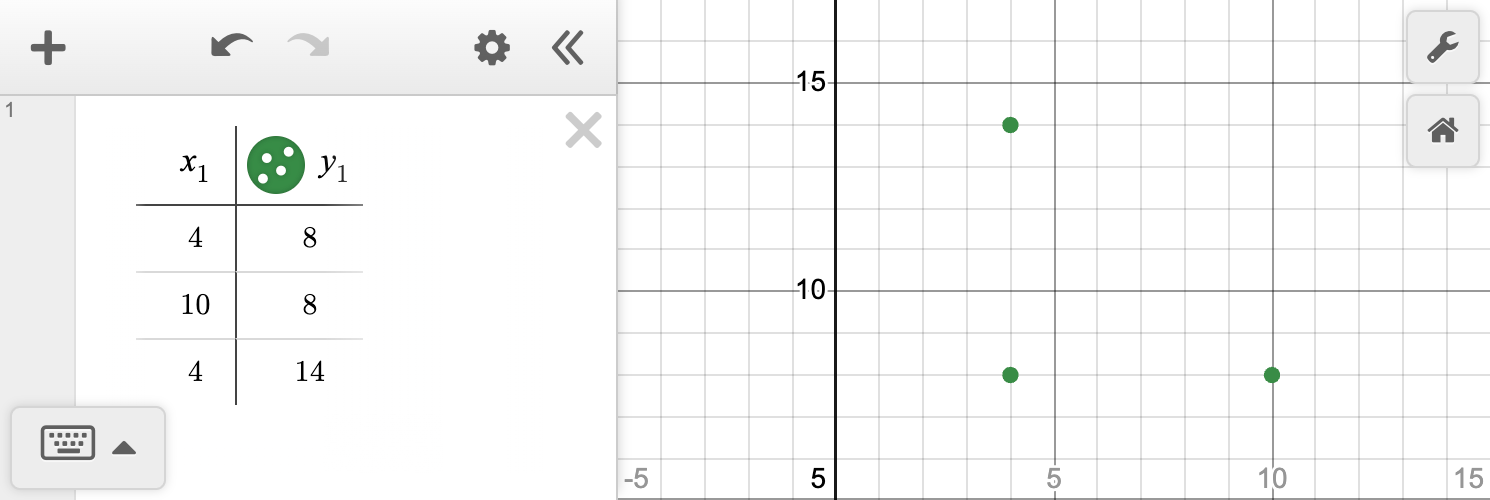
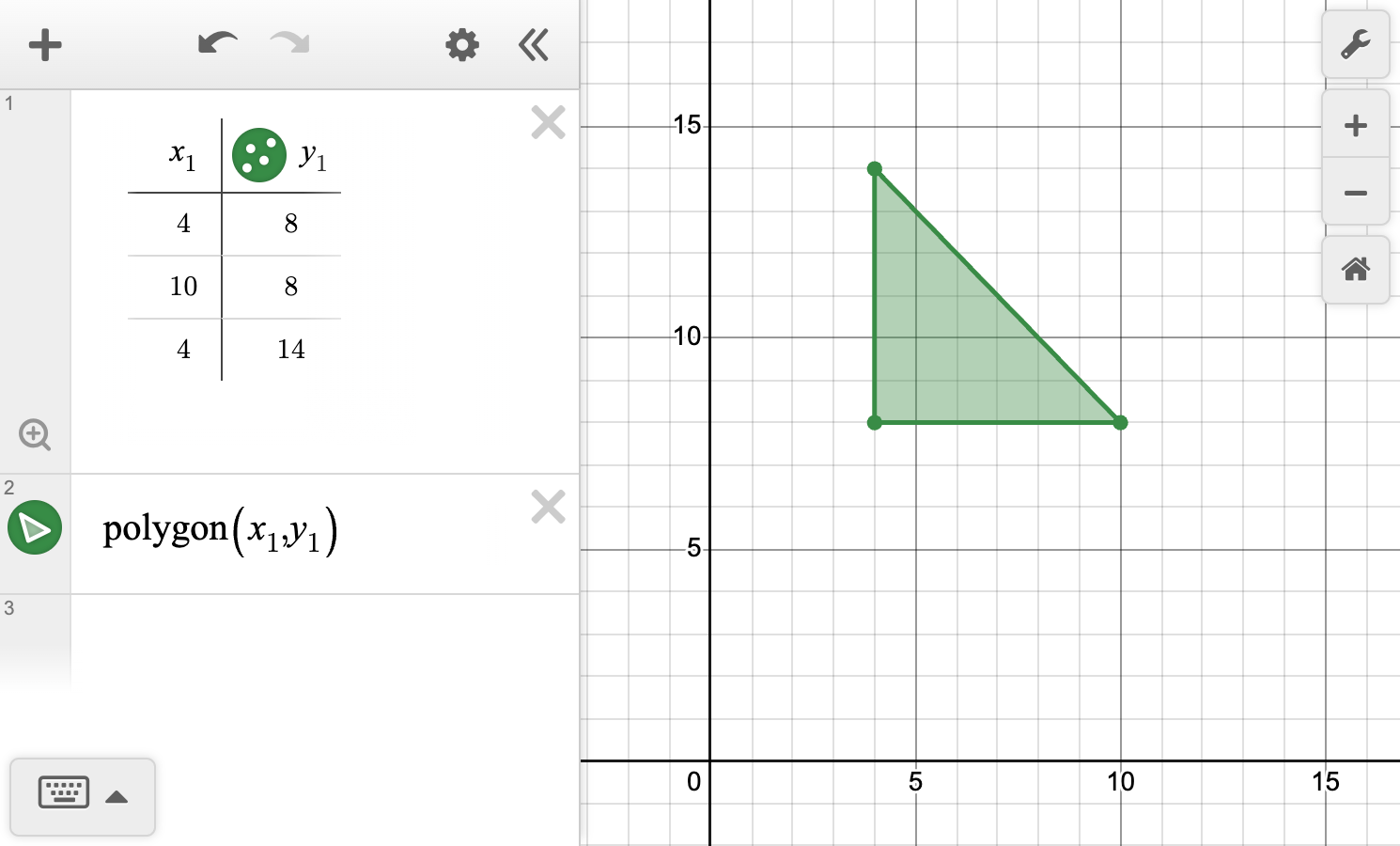
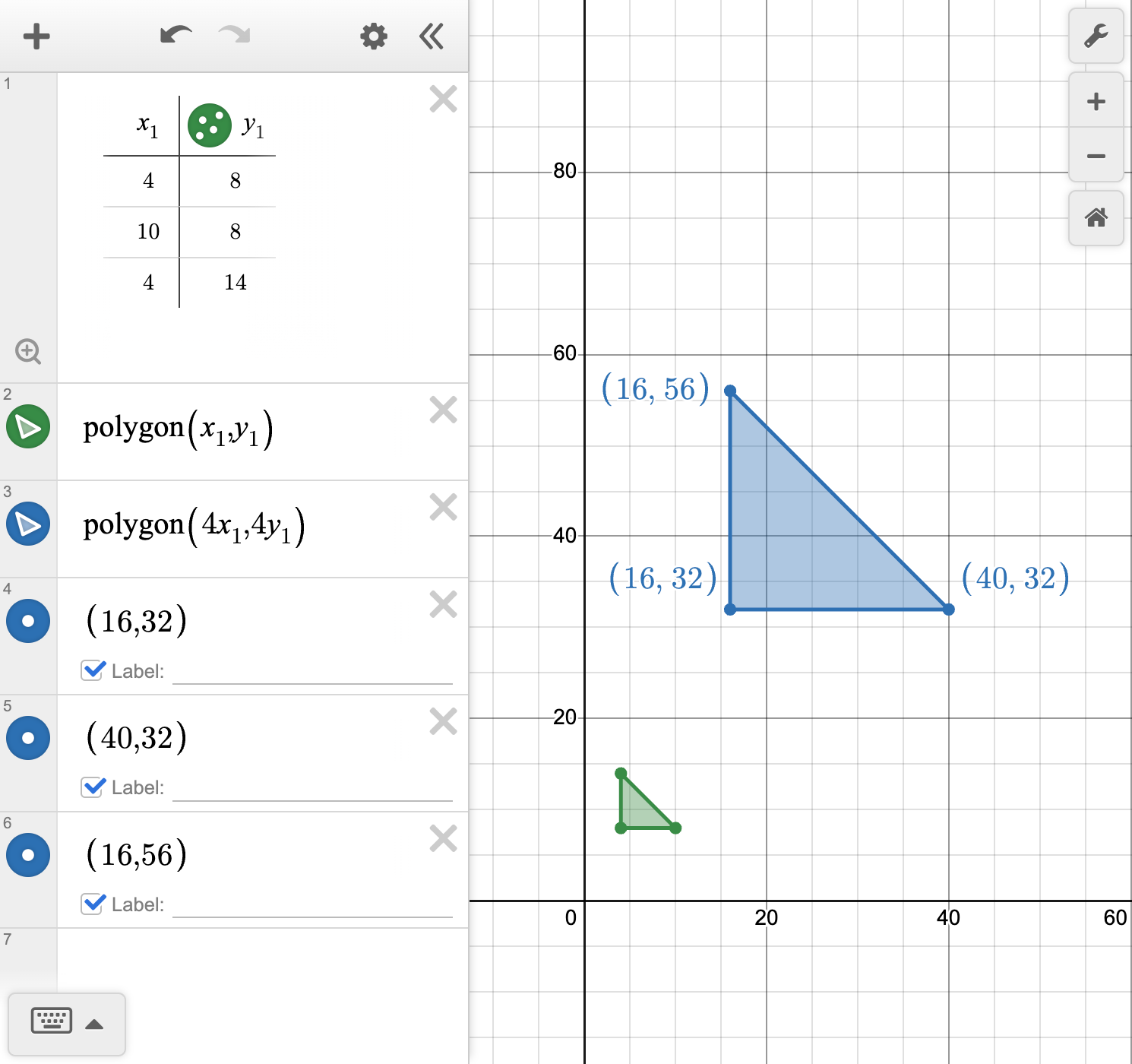
Consider the figure shown on the coordinate grid:

0
5
10
15
x
5
10
15
y
a

Dilate the figure using the rule \left(x,y\right) \to \left(4x, 4y\right).

Worked Solution
Create a strategy

Since the center of dilation is the origin, \left(0,0\right), and the scale factor is 4 based on the coordinate mapping, we can take the coordinates of each point in the preimage and multiply them by the scale factor to get the vertices of the image.

Apply the idea

We have:

\left(4, 8\right) \to \left(16, 32\right)

\left(10, 8\right) \to \left(40, 32\right)

\left(4, 14\right) \to \left(16, 56\right)

-5
5
10
15
20
25
30
35
40
45
50
55
x
-5
5
10
15
20
25
30
35
40
45
50
55
y
Reflect and check

We can verify the coordinates of the image using technology.

  1. In the Desmos graphing calculator, click the plus icon in the top left and then 'table' to add a table of values.

    A screenshot of the Desmos graphing calculator showing how to add a table. Ask your teacher for more information.

  2. Type the x-coordinates of the vertices of the preimage into the x_1 column of the table. Type the y-coordinates of the vertices of the preimage into the y_1 column of the table.

    A screenshot of the Desmos graphing calculator showing how to enter the coordinates of a polygon into a table. Ask your teacher for more information.

  3. In a new input line, type '\text{polygon}(x_1,y_1)' to graph the polygon using the points from the table.

    A screenshot of the Desmos graphing calculator showing how to create a polygon from a given set of coordinates in a table. Ask your teacher for more information.

  4. In a new input line, type '\text{polygon}(4x_1,4y_1)' which represents the coordinate form of the translation.

    A screenshot of the Desmos graphing calculator showing how to transform a polygon using coordinate notation. Ask your teacher for more information.

By entering the coordinates of the image, we can verify that the coordinates of the image match the ones we found.

b

Describe how the preimage and its image are related.

Worked Solution
Create a strategy

Using the figure and its image, connect the corresponding vertices of the preimage and image. Also, compare corresponding segments between preimage and image.

Apply the idea
-5
5
10
15
20
25
30
35
40
45
50
55
x
-5
5
10
15
20
25
30
35
40
45
50
55
y

We would expect that the image would be 4 times farther from the center of dilation than the preimage is, which appears to be true based on the graph.

We should also expect the segment lengths of A'B'C' to be 4 times longer than the corresponding segments of ABC. We can spot check one of the segments to verify this:AB = 10 - 4 = 6 \text{ and } A'B' = 40-16 = 24 \text{ and } 6 \cdot 4 = 24

We can see that corresponding segments are parallel to one another: \overline{AB} is a horizontal line with a slope of 0, as is \overline{A'B'}. We can see both \overline{AC} and \overline{A'C'} are vertical with no slope. Both \overline{CB} and \overline{C'B'} are decreasing lines with a slope of -1.

Example 2

Find the scale factor for the following dilation:

Two parallelograms are drawn. Parallelogram A B C D has side B C of length 16 and side D C of length 32. Segment A B and segment D C are marked parallel as well as segment B C and segment A D. Parallelogram A prime B prime C prime and D prime has side B prime C prime of length 2 and segment D prime C prime of length 4.
Worked Solution
Create a strategy

We can see that the preimage has side lengths of 32 and 16, and the image has side lengths of 4 and 2. This indicates that the preimage has been reduced. To find the scale factor we can divide one of the lengths of the image by the corresponding side length of the preimage.

Apply the idea

\dfrac{C'D'}{CD}=\frac{4}{32} Simplifying the quotient gives a scale factor of \dfrac{1}{8}.

Example 3

Consider the figure on the coordinate plane shown:

0
1
2
3
4
5
6
7
8
9
10
11
12
x
1
2
3
4
5
6
7
8
9
10
11
12
y
a

Dilate the figure around center of dilation \left(6,7\right) with a scale factor of \dfrac{1}{2}.

Worked Solution
Create a strategy

We can determine the translation from each vertex to the center of dilation, then apply the scale factor to the translations.

Apply the idea

  1. Determine the translations from the center of dilation to the vertices of the figure:

    • \left(6,7\right)\to\left(2,1\right): translate 4 units left and 6 units down

    • \left(6,7\right)\to\left(8,3\right): translate 2 units right and 4 units down

    • \left(6,7\right)\to\left(12,9\right): translate 6 units right and 2 units up

    • \left(6,7\right)\to\left(4,11\right): translate 2 units left and 4 units up

  2. Multiply these translations by the scale factor, \dfrac{1}{2}, to find the images of these points under the dilation in relation to the center of dilation:

    • Translate 2 units left and 3 units down

    • Translate 1 unit right and 2 units down

    • Translate 3 units right and 1 unit up

    • Translate 1 unit left and 2 units up

  3. Apply these translations to the center of dilation, \left(6,7\right), to determine the coordinates of the images of the vertices under dilation:

    • Translating \left(6,7\right) by 2 units left and 3 units down gives us \left(4,4\right)

    • Translating \left(6,7\right) by 1 unit right and 2 units down gives us \left(7,5\right)

    • Translating \left(6,7\right) by 3 units right and 1 unit up gives us \left(9,8\right)

    • Translating \left(6,7\right) by 1 unit left and 2 units up gives us \left(5,9\right)

  4. Plot the image of the dilation, using the images of the vertices determined in the previous step.

    0
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    x
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    y
b

Compare the preimage with its image after performing the dilation.

Worked Solution
Create a strategy

Use the figure and its image sketched in part (a) and what we know about dilating a figure around a central point.

Apply the idea

The preimage and its image have the same orientation. The preimage and its image are not congruent because the side lengths of the image are not preserved with a dilation.

The side lengths of the image are parallel to the side lengths of the preimage.

Since all corresponding side lengths are parallel, each pair of corresponding interior angles will be congruent.

The scale factor is \dfrac{1}{2}, meaning that the side lengths of the image should be half the length of the preimage side lengths. This visually appears to be true.

The distance between the center of a dilation and any point on the image appears to be equal to half of the distance between the dilation center and the corresponding point on the preimage, shown on the grid below.

0
1
2
3
4
5
6
7
8
9
10
11
12
x
1
2
3
4
5
6
7
8
9
10
11
12
y
Reflect and check

We could use a ruler and protractor to verify:

  1. corresponding segments are an equal distance apart (thus parallel)

  2. the length of each segment on the image is \dfrac{1}{2} the size of the corresponding segment of the preimage

  3. corresponding angles are congruent

These steps would verify that we have dilated the figure correctly.

Idea summary

When a figure is dilated with a center of dilation at point P by a factor of k:

  • The distance between P and any point on the image will be k times the size of the distance between P and the corresponding point on A.

  • The length of the image segments will be k times the size of the corresponding segment lengths of A.

  • When P is not a point on A, the image will be parallel to A.

  • When P lies on a line segment of A, its image will lie on the same line.

In coordinate notation, a point dilated with respect to the origin and a scale factor of k is written as \left(x,y\right)\to\left(kx,ky\right).

Outcomes

G.RLT.3ci

Given an image or preimage, identify the transformation or combination of transformations that has/have occurred. Transformations include: i) translations;

G.RLT.3civ

Given an image or preimage, identify the transformation or combination of transformations that has/have occurred. Transformations include: iv) dilations, from a fixed point on a coordinate grid.

G.TR.3

The student will, given information in the form of a figure or statement, prove and justify two triangles are similar using direct and indirect proofs, and solve problems, including those in context, involving measured attributes of similar triangles.

What is Mathspace

About Mathspace