6.03 SSS and SAS congruence criteria
Interactive practice questions
Consider the adjacent figure:
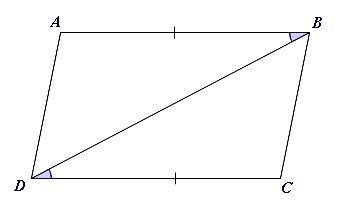
A quadrilateral labeled $ABCD$ABCD with vertices $A$A, $B$B, $C$C, and $D$D has a diagonal $BD$BD drawn. The top side $AB$AB and bottom side $CD$CD are marked with single tick marks suggesting they are of equal length. The diagonal $BD$BD is drawn from top right vertex $B$B to bottom left vertex $D$D and divides the angles on vertices $B$B and $D$D into two; forming angles $\angle ABD$∠ABD and $\angle CBD$∠CBDat vertex $B$B, and $\angle BDC$∠BDC and $\angle ADB$∠ADB at vertex $D$D. Diagonal $BD$BD also divides the quadrilateral into two triangles $\triangle ABD$△ABD and $\triangle CDB$△CDB where the diagonal $BD$BD is the common side shared by both triangles. Sides $AB$AB and diagonal $BD$BD forms an included angle $\angle ABD$∠ABD that is marked with a blue arc. Sides $CD$CD and diagonal $BD$BD forms an included angle $\angle BDC$∠BDC that is also marked with a blue arc marking.
From the information given on the diagram, which angle is congruent to $\angle ABD$∠ABD?
$\angle BAD$∠BAD
$\angle CDB$∠CDB
$\angle BCD$∠BCD
$\angle DBC$∠DBC
State the most direct reason why $\triangle ADB$△ADB is congruent to $\triangle CBD$△CBD.
AAS: A pair of corresponding angles and a non-included side are congruent.
SAS: A pair of corresponding sides and the included angle are congruent.
SSS: All three corresponding sides are congruent.
HL: Two right triangles with hypotenuse and one leg are congruent.
ASA: A pair of corresponding angles and the included side are congruent.
Consider the adjacent figure:
Consider the following diagram:
Consider the following diagram: