Topics
5. Rigid Transformations
topic badge
United States of AmericaVA
Geometry

5.02 Reflections

Lesson
Practice

Reflections

Exploration

Drag the points to create a triangle. Check the boxes to show the line of reflection, image, and movement of points. Drag the sliders to change the line of reflection.

Loading interactive...
  1. What happens to the image as you move the line of reflection?
  2. What do you notice about the angle formed by the segments from the preimage to the image and the line of reflection?
  3. What can we say about the distance of each figure to the line of reflection?

We can think of a reflection as a function which sends the input point to an output point so that both points are equidistant from the line of reflection. This means that the midpoint of the segment that connects these two points lies on the line of reflection.

Reflection

A transformation that produces the mirror image of a figure across a line.

Line of reflection

A line that a figure is flipped over to create a mirror image.

In other words, the line of reflection is always the perpendicular bisector of the line segment joining corresponding points in the preimage and image. Because of this, the line of reflection will always be equidistant from the two corresponding points in the preimage and image, so we get a mirror image over the line of reflection.

-4
-3
-2
-1
1
2
3
4
x
-4
-3
-2
-1
1
2
3
4
y

The most common lines of reflection have the following impact on a point:

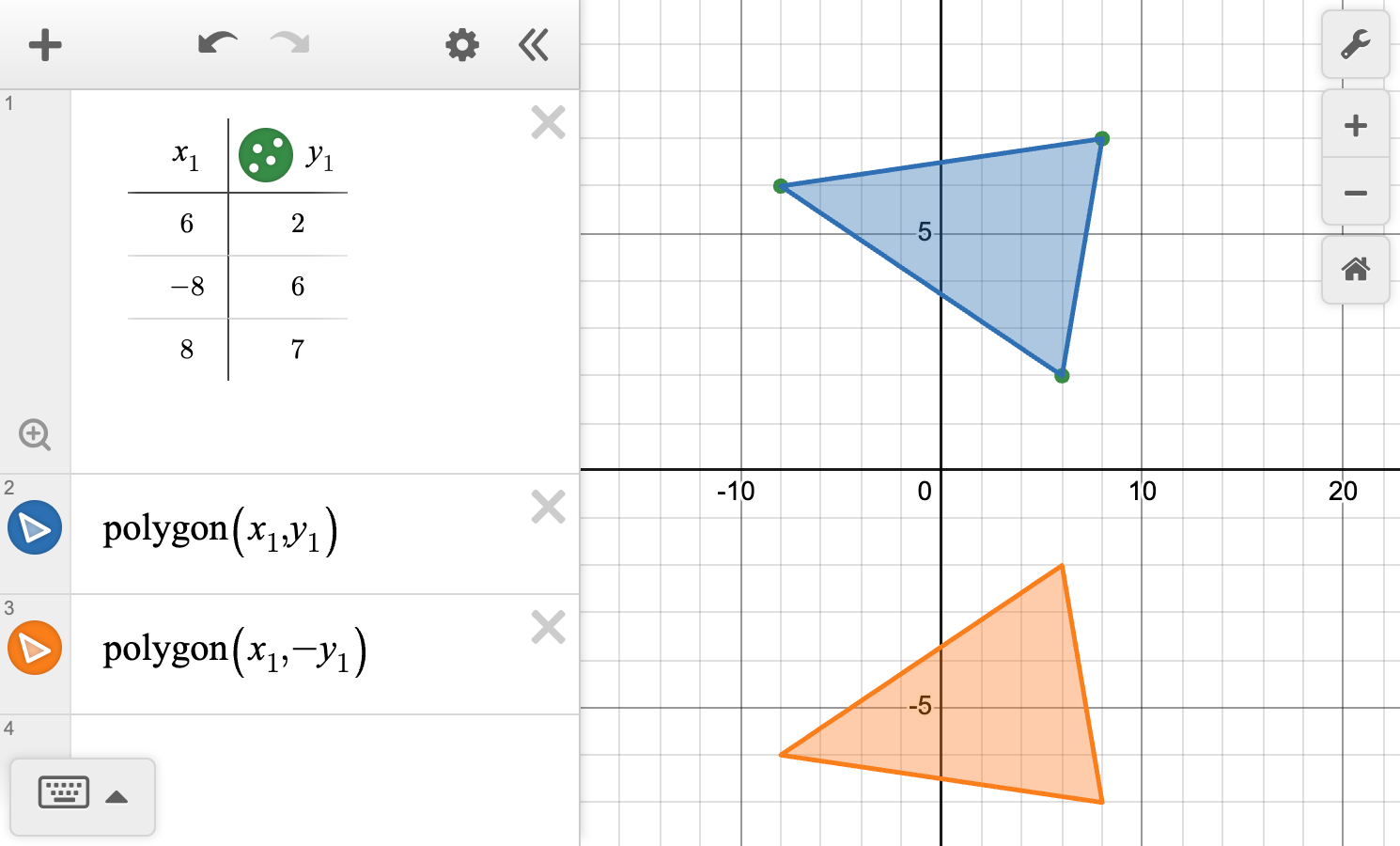
  • Line of reflection: x-axis \qquad Coordinate mapping: \left(x, y\right) \to \left(x, -y \right)

  • Line of reflection: y-axis \qquad Coordinate mapping: \left(x, y\right) \to \left(-x, y \right)

  • Line of reflection: y=x \, \, \qquad Coordinate mapping: \left(x, y\right) \to \left(y, x \right)

  • Line of reflection: y=-x \, \, \, \quad Coordinate mapping: \left(x, y\right) \to \left(-y, -x \right)

Examples

Example 1

For the given graph:

-8
-4
4
8
x
-6
-4
-2
2
4
6
y
a

Identify the line of reflection.

Worked Solution
Create a strategy

The line must be equal distance between the pairs A and A',\,B, and B', and C and C'. So, to find the line of reflection, we can connect the vertices and find the midpoints.

Apply the idea

Connect the vertices and plot the midpoints:

-8
-4
4
8
x
-6
-4
-2
2
4
6
y

Draw the line of reflection through the midpoints:

-8
-4
4
8
x
-6
-4
-2
2
4
6
y

The line of reflection goes through all of the midpoints. Therefore, the line of reflection is the x-axis, y=0.

Reflect and check

We can use the midpoint formula to find the midpoint between each of the vertices.

Midpoint of A andA':

x_{m}=\dfrac{x_{1}+x_{2}}{2}= \dfrac{6+6}{2} =6

y_{m}=\dfrac{y_{1}+y_{2}}{2}= \dfrac{2+\left(-2\right)}{2} =0

The midpoint of vertices A and A' is \left(6,0\right).

Calculating the midpoint for the other vertices, we would have \left(-8,0\right) for B and B' and \left(8,0\right) for C and C'.

The midpoints all have the same y-coordinate, so the line that passes through them all has the equation y=0.

b

Write the transformation mapping in coordinate notation.

Worked Solution
Create a strategy

The reflection mapping is given by the change in the coordinates of a point \left(x,y\right) from the preimage to the image.

Apply the idea

Observe how the coordinates of A \left(6,2\right) and A'\left(6,-2\right) have opposite y-values but the x-values are the same.

  • Point A\left(6,2\right) is reflected to point A'\left(6,-2\right)

  • Point B\left(-8,6\right) is reflected to point B'\left(-8,-6\right)

  • Point C\left(8,7\right) is reflected to point C'\left(8,-7\right)

Coordinate notation: \left(x,y\right) \to \left(x,-y\right)

Reflect and check

We can verify the coordinate notation of the transformation using technology.

  1. In the Desmos graphing calculator, click the plus icon in the top left and then 'table' to add a table of values.

    A screenshot of the Desmos graphing calculator showing how to add a table. Ask your teacher for more information.

  2. Type the x-coordinates of the vertices of the preimage into the x_1 column of the table. Type the y-coordinates of the vertices of the preimage into the y_1 column of the table.

    A screenshot of the Desmos graphing calculator showing how to enter the coordinates of a polygon into a table. Ask your teacher for more information.

  3. In a new input line, type '\text{polygon}(x_1,y_1)' to graph the polygon using the points from the table.

    A screenshot of the Desmos graphing calculator showing how to create a polygon from a giving set of coordinates in a table. Ask your teacher for more information.

  4. In a new input line, type '\text{polygon}(x_1,-y_1)' which represents the coordinate form of the translation.

    A screenshot of the Desmos graphing calculator showing how to transform a polygon using coordinate notation. Ask your teacher for more information.

The original polygon has been reflected across the x-axis, which matches the given image and transformation. This verifies our coordinate notation.

Example 2

Determine the image of the quadrilateral PQRS when reflected across the line y=-x.

-4
-3
-2
-1
1
2
3
4
x
-4
-3
-2
-1
1
2
3
4
y
Worked Solution
Create a strategy

We can use a mirror or tracing paper to map each vertex of the preimage to its image across the line.

Apply the idea

Reflecting each point, we get the following mapping:

  • The point P\left(1,1\right) is reflected to P'\left(-1,-1\right)
  • The point Q\left(3,3\right) is reflected to Q'\left(-3,-3\right)
  • The point R\left(3,2\right) is reflected to R'\left(-2,-3\right)
  • The point S\left(2,0\right) is reflected to S'\left(0,-2\right)

Plotting these points and connecting them gives us the image:

-4
-3
-2
-1
1
2
3
4
x
-4
-3
-2
-1
1
2
3
4
y
Reflect and check

By comparing the coordinates of the points from the preimage to the image, we can see the rule for reflecting across the line y=-x is \left(x,y\right) \to \left(-y,-x\right)

Example 3

A new housing development is being built so that each property is a mirror image of the one next door. Here are the plans for 2 neighboring properties. Using geometric construction, draw the property line between the two houses.

aerial view of 2 houses that are refections. A point is in the same spot on each house.
Worked Solution
Create a strategy

The property line should divide the plot of land into two equal sized and symmetric plots. A perpendicular bisector will do this for us.

To construct a perpendicular bisector, we can use a compass and straight edge.

Apply the idea

Step 1: Identify the segment we want to bisect. Make sure to use corresponding points on each of the houses.

Aerial view of 2 houses that are refections. A point is in the same spot on each house. A line connecting the two points is drawn.

Step 2: Open the compass width to just past half the segment's length and draw an arc from one endpoint that extends to both sides of the segment. Repeat with same width for other endpoint.

Aerial view of 2 houses that are refections. A point is in the same spot on each house. A line connecting the two points is drawn. Arcs are drawn using each point as the vertex, intersecting the straight line.

Step 3: Label the intersection of the arcs with points.

Aerial view of 2 houses that are refections. A point is in the same spot on each house. A line connecting the two points is drawn. Arches are drawn using each point as the vertex, intersecting the straight line. Points are drawn on the intersections of the arcs

Step 4: Connect the points to draw the property line.

Aerial view of 2 houses that are refections. A point is in the same spot on each house. A line connecting the two points is drawn. Arches are drawn using each point as the vertex, intersecting the straight line. Points are drawn on the intersections of the arcs, a line is drawn passing through these points.
Reflect and check

Constructing the perpendicular bisector creates a line of reflection. This ensures that the corresponding points on each property are the same distance from the property line.

Idea summary

The most common lines of reflections have the following impact on a point:

  • Line of reflection: x-axis \qquad Transformation mapping: \left(x, y\right) \to \left(x, -y \right)

  • Line of reflection: y-axis \qquad Transformation mapping: \left(x, y\right) \to \left(-x, y \right)

  • Line of reflection: y=x \, \, \qquad Transformation mapping: \left(x, y\right) \to \left(y, x \right)

  • Line of reflection: y=-x \, \, \, \quad Transformation mapping: \left(x, y\right) \to \left(-y, -x \right)

Outcomes

G.RLT.3

The student will solve problems, including contextual problems, involving symmetry and transformation.

G.RLT.3ci

Given an image or preimage, identify the transformation or combination of transformations that has/have occurred. Transformations include: i) translations;

G.RLT.3cii

Given an image or preimage, identify the transformation or combination of transformations that has/have occurred. Transformations include: ii) reflections over any horizontal or vertical line or the lines y = x or y = -x;

What is Mathspace

About Mathspace