5.09 Graphs of exponential functions
Graphs of exponential functions
To draw the graph of an exponential function, we can use a variety of strategies, including:
- Completing a table of values for the function and drawing the curve through the points found
- Using technology, such as a physical or online graphing calculator
- Identifying transformations from the equation
Exploration
The graph of y=2^x is shown. Slide the two sliders to transform the graph of y=a\left(2\right)^x+k.
Which variable(s) change the horizontal asymptote?
Which variable(s) change the shape of the graph?
Which variable(s) change the y-intercept?
Set the k slider to k=0. Describe the graph when a is positive. Describe the graph when a is negative.
Set the a slider to a=1. Describe what happens when k is positive. Describe what happens when k is negative.
An exponential function could also undergo transformations based on the leading coefficient, a, and vertical shift, k:
The y-intercept is the value of a. We can check this by substituting x=0 in the function: y=ab^0. Since b^0=1, the y-intercept is (0,\,a).
For k \gt 0, the graph will shift up k units. For k \lt 0, the graph will shift down k units.
The key features of an exponential function can be found in both the equation and the graph.
Given f(x)=ab^x, the leading coefficient, a, represents the y-intercept and is plotted as the point (0,\,a). It also determines the range of the function.
- When a \gt 0, the range is y \gt 0
- When a \lt 0, the range is y \lt 0.
The value of a also affects the rate of change of the function. If two functions have the same value for b, a larger value for a will have a greater rate of change.
The absolute value of a, tells us whether the graph's height will be made taller or shorter.
If \left\vert a \right\vert \gt 1, then every y-coordinate of the function is multiplied by a factor a that is greater than 1. The points on the graph move further away from the x-axis, increasing the steepness of the graph. This is called a vertical stretch.
If 0\lt \left\vert a \right\vert \lt 1, then every y-coordinate of the function is multiplied by a factor a that is between 0 and 1. The points on the graph move closer to the x-axis, decreasing the steepness of the graph. This is called a vertical compression.
Examples
Example 1
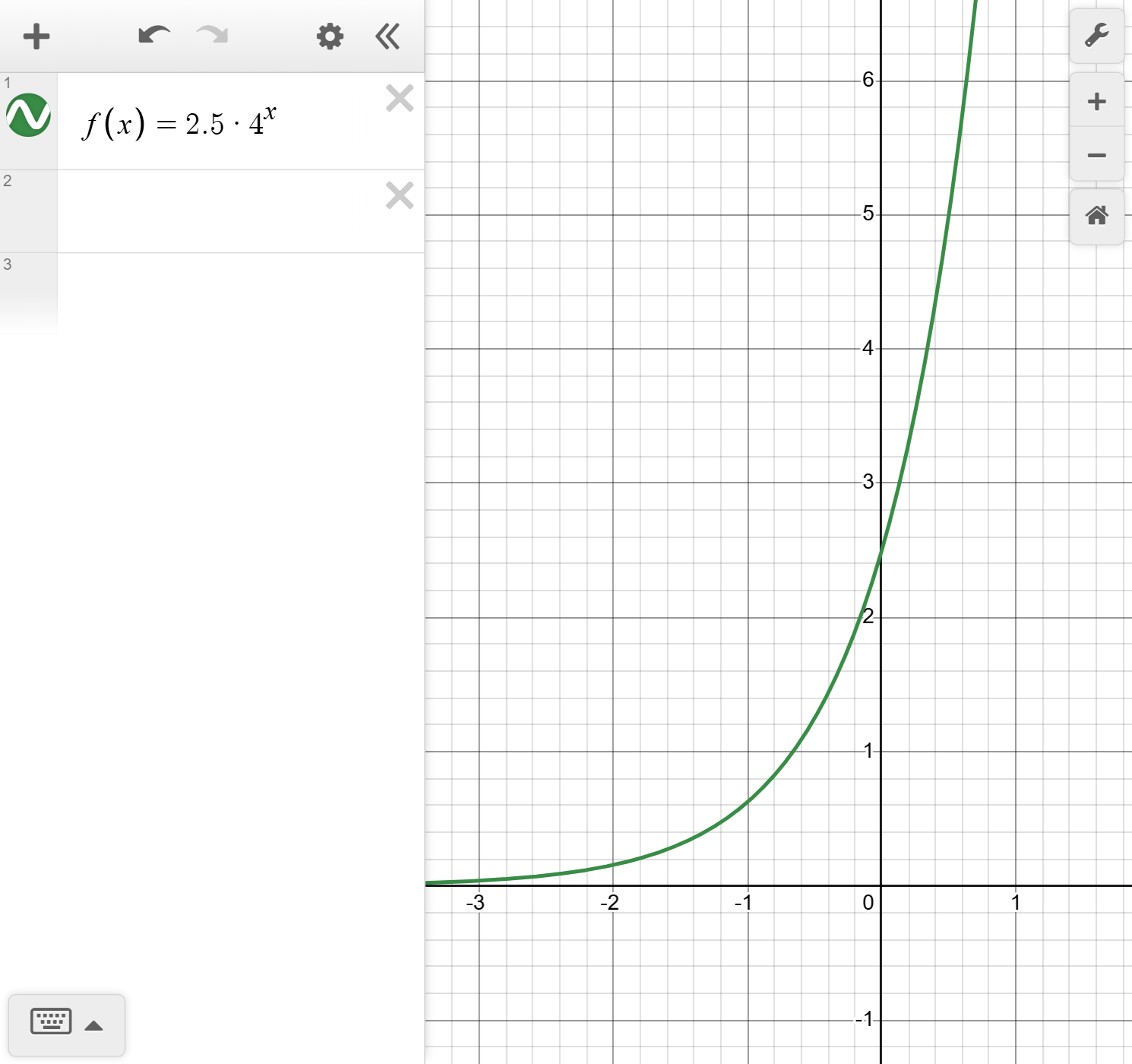
Consider the exponential function y=2.5\left(4\right)^x.
Draw the graph of the function.
Check the graph from part (a) using technology.
Without graphing, how would you expect this graph to look different than the graph of y = (4)^x
Example 2
In 2010, Bob counted 3 rabbits in his backyard. He noticed they double every week. Let f(x) describe this scenario, and use it to answer the questions below.
Find the y-intercept.
Write an equation describing this scenario.
Graph the function.
Example 3
Consider the function y=-4^{x} - 1:
Find the y-intercept.
Graph the function as a transformation of the function f(x) = -4^x.
We can use the y-intercept, the constant factor, b, and the vertical shift, k. to graph an exponential function in the form y=ab^x + k and identify key features:
- When a \gt 0 and b \gt 1, the function is increasing at an increasing rate.
- When a \lt 0 and b \gt 1, the function is decreasing at an increasing rate.
- k \gt 0, will shift the graph k units up.
- k \lt 0, will shift the graph k units down.