Mixed graphs II (linear, quad, cubic, 1/x)

Reviewing some basic graph types

Let's first recall the basic graphs as shown here in the diagram. The function's description is given below each graph. For example the linear function $$y=mx+b is shown on the left and the hyperbola $$y=1x​ is shown second from right. 

Two of the graphs are shown with some generalising coefficients - the line $$y=mx+b and the exponential curve  $$y=ax. Thus we could site particular examples of these graphs such as $$y=2x+5, $$y=7x and $$y=3x etc.

However, all of these basic types can be generalised further by what are known as transformations.

Translations

One common transformation is known as a translation.  This is a horizontal and/or vertical shift in the position of the curve relative to the cartesian axes. Translations are easy to recognise.

If we replace $$x with $$(x−h), the basic curve is moved $$h units to the right. If we replace $$x with $$(x+h), the basic curve is moved $$h units to the left. If we replace $$y with $$(y−k), the basic curve is moved $$k units up. If we replace $$y with $$(y+k), the basic curve is moved $$k units down. 

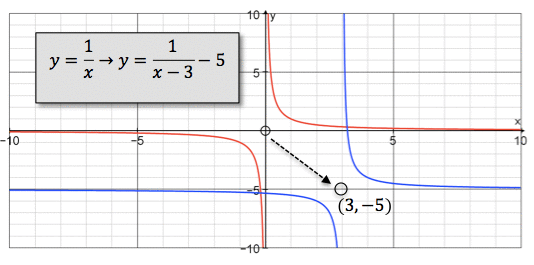
So suppose we take the hyperbola $$y=1x​ and translate it $$3 units to the right and $$5 units down. The new function becomes $$y+5=1x−3​, or expressed explicitly $$y=1x−3​−5. The vertical and horizontal asymptotes are respectively $$x=3 and $$y=−5.

If we take the parabola $$y=x2 and shift it $$1 unit to the left and $$5 units up, the new function becomes $$y−5=(x−1)2 . Again, we can express this explicitly as $$y=(x−1)2+5. 

If we take the function $$y=x3 and translate it $$2 units to the right and $$1 unit up, the new function is given by $$y−1=(x−2)3, expressible as $$y=(x−2)3+1. 

Dilations and reflections

Another type of transformation is commonly referred to as a dilation. This is when a curve is stretched or compressed by some factor other than $$1 in the function's equation.

For example, the difference between $$y=x2 to $$y=3x2 is the dilation factor $$3. Every function value in $$y=3x2 is $$3 times the associated function value in $$y=x2. This means that the curve becomes steeper.

Again, every function value of the function $$y=2x​ is double the associated function value of $$y=1x​.

Every function value of $$y=3(2x) is $$3 times that of $$y=2x, and every function value of $$y=12​x3 is one-halve that of $$y=x3.

We can also reflect a curve across the $$x - axis by simply multiplying its function expression by $$−1.

Every function value of $$y=−x2 is the negative of those of $$y=x2, and the curve becomes an upside-down parabola with the same vertex as $$y=x2. Again, every function value of $$y=−3x​ is the reflected image of across the x -axis of $$y=3x​.  

 

Combining Translations and dilations

When we combine translations and dilations we can reposition and distort the basic curve. 

For example, the curve of $$y=5x−2​+3 is constructed as follows. Start with the curve given by the basic function $$y=1x​ and stretch each ordinate by a factor of $$5. Then shift it $$2 units to the right  and $$3 units up, so that the centre becomes $$(2,3)  with the curve's asymptotes as  $$x=2 and $$y=3.

The final graph is shown in red here, along with the graph of $$y=1x−2​+3. Note how changing from $$y=1x−2​+3 to $$y=5x−2​+3 pushes the hyperbola out diagonally. 

Finding $$x and $$y intercepts    

The $$y intercept of any function are found by putting $$x=0 into the equation. The $$x intercept(s) are found similarly by putting $$x=0. 

For example, for the curve given by $$y=1x−3​−5, putting $$x=0 reveals $$y=10−3​−5=−513​. 

The x intercept is found by putting $$y=0, so that $$1x−3​−5=0. This means that $$1x−3​=5 and inverting $$x−3=15​ so that $$x=315​.

 

 

 

Worked Examples

Question 1

Question 2

Question 3

Question 4