5.02 Direct and inverse variation
Direct variation
A direct variation represents a proportional relationship between two quantities. This means that one variable is always a constant multiple of the other.
For example, if you earn \$18 per hour, your earnings are directly proportional to the number of hours worked because \text{earnings}=18 \cdot \text{hours worked}. We would say hours worked and money earned are directly proportional.
The constant of proportionality \left(k\right), is the ratio of the dependent variable to the independent variable. So k=\dfrac{y}{x}.
We can also refer to this as the constant of variation. In the hourly earnings example, the constant would be 18.
A direct variation can be written in the form:
A very common misconception is that two variables are directly proportional if one increases as the other increases. This is not the case. We can only say that two variables are directly proportional if the ratio between the variables stays constant. In other words, both variables increase or decrease at a constant rate.
If we graph a direct variation, we will see a linear graph (straight line) that passes through the origin , \left(0,\,0\right).
The value of k can be any real number, including fractions and negative numbers.
Examples
Example 1
Consider P=90t
Find the constant of proportionality.
Find the value of P when t=2.
Example 2
If I pay \$6 for 12 eggs and \$10 for 20 eggs, are these rates directly proportional?
Example 3
Consider the values in each table. Which could represent a directly proportional relationship between x and y? Select all that apply.
Example 4
Ivan paints 10 plates every 6 hours.
Write an equation to represent this situation.
Use your equation to plot this situation on a coordinate plane.
A direct variation can be written in the form:
The graph of all points describing a direct variation is a straight line passing through the origin.
Inverse variation
Now that we know about direct variation we will look at inverse variation. Inverse variation means that as one amount increases the other amount decreases.
For example, speed and travel time are inversely proportional because the faster you go, the shorter your travel time.
We express these kinds of inversely proportional relationships generally in the form:
While the graph of a direct variation is linear, we can see the graph of an inverse variation is nonlinear.
Inverse variation is a subset of the rational function family with parent function y = \dfrac{1}{x}. Different constants of proportionality represent dilations. A negative constant of proportionality applys a reflection.
Examples
Example 5
Consider s=\dfrac{375}{t}
Find the constant of proportionality.
Find the value of s when t=6. Give your answer as an exact value.
Find the value of s when t=12. Give your answer as an exact value.
Example 6
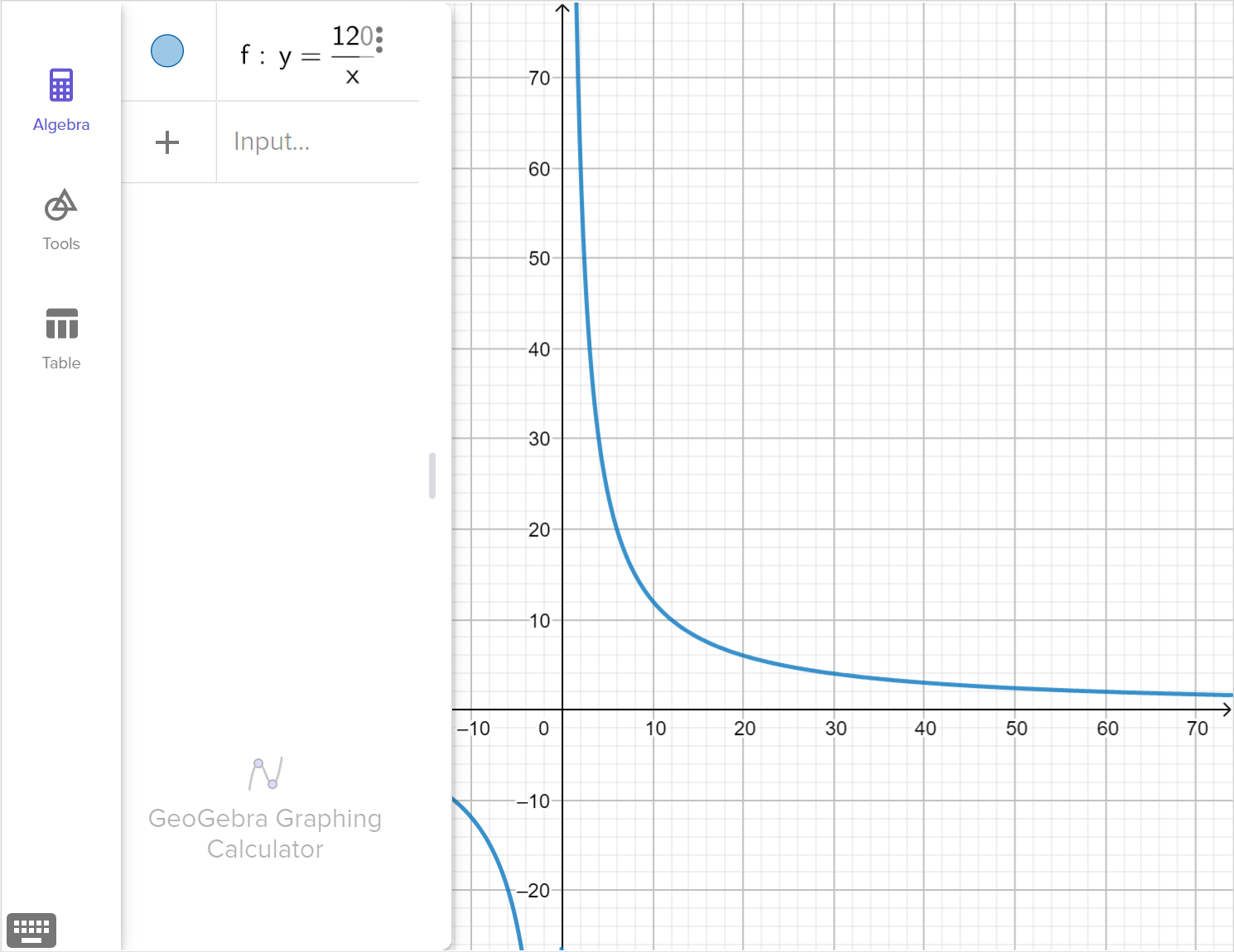
Consider the table of values.
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| y | 120 | 60 | 40 | 30 | 24 |
Determine whether the table of values could represent an inverse variation between x and y.
Write a function relating y and x, given the table of values.
Describe the behavior of the function as x \to 0 from the right, and describe the behavior of the function as x \to \infty.
Example 7
Is the variation relating the distance between two locations on a map and the actual distance between the two locations an example of a direct variation or an inverse variation?
We express inversely proportional relationships in the form: