The volume of a three dimensional shape is the amount of space that is contained within that shape.
A quantity of volume is represented in terms of the volume of a unit cube, which is a cube with side length $1$1 unit. By definition, a single unit cube has a volume of $1$1 cubic unit, written as $1$1 unit3.

1 unit cube has a volume of 1 unit3.
The image below shows a rectangular prism with length $5$5 units, width $3$3 units, and height $2$2 units. Notice that the length of each edge corresponds to the number of unit cubes that could be lined up side by side along that edge.

How many unit cubes fit within this shape?
We can find the number of unit cubes that could fit inside the rectangular prism by taking the product of the three side lengths. This gives $5\times3\times2=30$5×3×2=30, so there are $30$30 unit cubes in the prism, which means it has a volume of $30$30 unit3.
Volume of a rectangular prism
In the same way that the area of a two dimensional shape is related to the product of two perpendicular lengths, the volume of a three dimensional shape is related to the product of three mutually perpendicular lengths (each of the three lengths is perpendicular to the other two).
The volume of a rectangular prism is given by
$\text{Volume }=\text{length }\times\text{width }\times\text{height }$Volume =length ×width ×height , or
$V=l\times w\times h$V=l×w×h
A cube can be thought of as a special type of rectangular prism, one that has all sides equal in length. The formula for the volume of a cube is similar to the formula for the area of a square.
The volume of a cube is given by
$\text{Volume }=\text{side }\times\text{side }\times\text{side }$Volume =side ×side ×side , or
$V=s\times s\times s=s^3$V=s×s×s=s3
Worked examples
Example 1
Find the volume of the following rectangular prism.

Think: The side lengths have units of cm, so the volume will be in cm3.
Do: The base of the prism has a width of $2$2 cm and a length of $7$7 cm, and the height of the prism is $9$9 cm. We will use these sides in the formula for the volume of a rectangular prism.
| $\text{Volume }$Volume | $=$= | $\text{length }\times\text{width }\times\text{height }$length ×width ×height | (Formula for the volume of a rectangular prism) |
| $=$= | $7\times2\times9$7×2×9 | (Substitute the values for the length, width, and height) | |
| $=$= | $126$126 | (Perform the multiplication to find the volume) |
So this rectangular prism has a volume of $126$126 cm3.
Example 2
The local swimming pool is $25$25 m long. It has eight lanes, each $2$2 m wide, and its depth is $1.5$1.5 m. What is the volume of water in the pool?

Think: The water in the pool is in the shape of a rectangular prism, so to find its volume we need to find the side lengths of this prism. The length and depth of the pool are two side lengths we can use. The final side length is found by multiplying the number of lanes by the width of each lane.
Do: First we calculate the width of the pool using the width of each swim lane: $8\times2$8×2 m $=16$=16 m. Next we use the formula for the volume of a rectangular prism.
| $\text{Volume }$Volume | $=$= | $\text{length }\times\text{width }\times\text{height }$length ×width ×height | (Formula for the volume of a rectangular prism) |
| $=$= | $25\times16\times1.5$25×16×1.5 | (Substitute the values for the length, width, and height) | |
| $=$= | $600$600 | (Perform the multiplication to find the volume) |
So the water in the pool has a volume of $600$600 m3.
Reflect: Even though the volume formula uses the terms "length", "width", and "height", when referring to everyday objects it may be more appropriate or more common to use alternative words like "width", "depth", or "thickness". In this example, we could just as well have used the formula $\text{Volume }=\text{length }\times\text{width }\times\text{depth }$Volume =length ×width ×depth .
Practice questions
Question 1
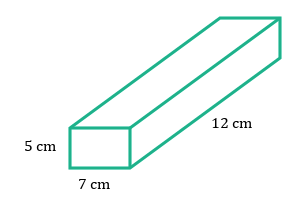
Find the volume of the rectangular prism shown.
To find the volume of a triangular prism, we can do as we did for the rectangular prism and find the number of squares that would cover the base (area of the base) multiplied by the height.

So the volume is:
$\text{Volume }=\text{Area of the triangle }\times\text{Height of the prism }$Volume =Area of the triangle ×Height of the prism
Since the prism can look quite different depending on the triangular face and which way it is orientated we need to be cautious about which measurements we use in our calculations.

To calculate the volume of a triangular prism we need the base and perpendicular height of the triangular face as well as the length of the prism - the distance between the two triangular faces, which is also referred to as the perpendicular height of the prism

Given these three measurements the volume of a triangular prism can be found as follows.
For triangular prisms:
$\text{Volume }=\text{Area of the triangle}\times\text{height of the prism}$Volume =Area of the triangle×height of the prism
Which we can simplify to $V=Ah$V=Ah.
Worked example
Example 3
Find the volume of the triangular prism shown.
Think: We want to identify the base and perpendicular height of the triangular face and the length of the prism. We can then use the formula: $\text{Volume }=\text{Area of triangle}\times\text{height of the prism}$Volume =Area of triangle×height of the prism.
Do:
| $V$V | $=$= | $\text{Area of triangle}\times\text{height of the prism}$Area of triangle×height of the prism |
Write down formula. |
| $=$= | $\left(\frac{1}{2}\times4\times3\right)\times6$(12×4×3)×6 |
Substitute in given lengths. |
|
| $=$= | $6\times6$6×6 |
Evaluate the area first |
|
| $=$= | $36$36 |
Evaluate the product to find the volume |
So the volume of the triangular prism is $36$36 cm2.
Reflect: We can see that in the case of both the rectangular prism, and the triangular prism, we first calculated the area of the flat base that makes up the shape, and then multiplied this by the height of the prism. There is nothing special about these two shapes, and in fact, we can find the volume of any prism using the same method. That is, if we know the area of the base and the height of the prism we can find the volume.
Volume of prisms
For all prisms:
$\text{Volume }=\text{Area of the base}\times\text{height of the prism}$Volume =Area of the base×height of the prism
Which we can simplify to $V=Ah$V=Ah.
Practice questions
Question 2
Find the volume of the figure shown.

A trapezoidal prism has its top trapezoidal face shaded in light green. The area of the top face is labeled as $A=30$A=30 cm². The height of the prism is labeled as $8$8 cm. The non-visible part of the prism is represented as dashed lines.
Question 3
Consider the prism shown in the diagram.

What is the shape of the base of this prism?
Parallelogram
ATriangle
BRectangle
CSquare
DFind the area of the prism's base.
Find the volume of the prism.
Cylinders
A cylinder is very similar to a prism (except for the lateral face), so the volume can be found using the same concept we have already learnt.
| $\text{Volume of Cylinder }$Volume of Cylinder | $=$= | $\text{Area of Base }\times\text{Height of Prism}$Area of Base ×Height of Prism |
| $\text{Volume of Cylinder }$Volume of Cylinder | $=$= | $\pi r^2\times h$πr2×h |
| $\text{Volume of Cylinder }$Volume of Cylinder | $=$= | $\pi r^2h$πr2h |
Practice questions
Question 4
Consider the solid shown in the diagram.

What is the shape of the base of this solid?
Cylinder
ASemicircle
BRectangle
CCircle
DFind the exact area of the solid's base. Leave your answer in terms of $\pi$π.
Find the exact volume of the solid. Leave your answer in terms of $\pi$π.
Question 5
Find the volume of the cylinder rounded to two decimal places.


